Stark Effect

Stark Effect has a number of MP3 tracks up ranging from We Like Repartee (dictionaraoke -- songs sung by the pronunciation guides from online dictionaries) to Wonderbottle (Christina Aguilera Genie in a Bottle vs. Oasis Wonderwall). Take a look.

Del.icio.us

Even Spammers Need Subsidising

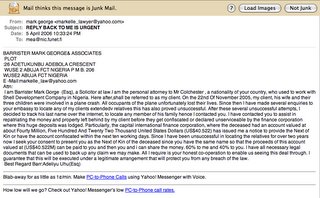Even spammers, it would seem, need to subsidise their operations with advertising. In the screen capture above, you can see that this Nigerian scam email has a couple of ads (for Yahoo! messenger) appended to it. This is probably the result of some bit of filth spammer sending their message from Yahoo!'s web-mail service to an e-mail list instead of doing the job properly. It appears as though spammers standards, low though they have always been, are slipping.

Order of Operations

A recent experience reminded me of some posts on Math and Text, a blog on mathematics education. So Long, Aunt Sally! discusses mnemonic devices for the order of operations (and reasons that such are a Bad Thing^(TM)) and Order of Operations motivates the standard order of operations in terms of error reduction (performing those operations which will most effect the magnitude of the result first will reduce our error in the event that we've misread a number).

Both of these posts interest me as I think that they both contain within them interesting insights to mathematics as seen by most of us (the non-mathematicians). The standard mathematical notation (that is, infix operators interpreted according to the standard order of operations) has a long history and is very much embedded with our understanding of maths. Unfortunately it is also rather poorly suited to expressing complex sentences: it requires that we interpret sentences with respect to a specific order of operations (exponentiation, multiplication/division, addition/subtraction) and use grouping operators (parentheses, brackets and the like).

This shortcoming is, however, addressed in a class of expression languages called prefix and postfix languages. The difference between an infix language (like the standard mathematical notation), a prefix language and a postfix language is suggested by their names. An infix language situates operators in-between their arguments, a prefix language writes operators before their arguments and a in postfix language the operators follow their arguments.

Where there is an ambiguity in infix languages as to which operators ought to be evaluated first (Left-to-right? Inward? Outward? According to precedence?), sentences of pre- and post-fix languages have only one possible interpretation. In these languages operations are performed in the order that they are written and we can express every sentence without using grouping operators (like brackets).

In an infix language, the sentence "1+2*3" is ambiguous and can be parsed in two different ways: "(1+2)*3" and "1+(2*3)" (see figure 1). Without a system of operator precedence, there is no way in which we can determine which of these two interpretations is "correct." In a pre- or post-fix language however, these two different interpretations are actually written differently. In postfix form, they can be written as "1 2 + 3 *" and "1 2 3 * +" respectively.

Figure 1: Parse trees for the sentence "1+2*3" with main operator being + (left) and * (right).

As they don't need an operator precedence scheme to determine which possible interpretation, these languages are much easier to parse and evaluate. This makes them ideal for use in constrained environment like calculators and printers. It is no surprise then, that many printers use the language Postscript to describe documents to be printed (with operators like draw-line and change colour, in addition to add and multiply) and some calculators use a programming language called RPN (though newer calculators also provide more complete languages).

The algorithm for evaluating an expression is postfix form is:

1. Read a token;
2. If it's a value push it onto the stack;
3. If it is an operator:
   1. Pop the appropriate number of arguments off the stack;
   2. Perform the operation on those arguments; and
   3. Push the result of the operation onto the stack
4. Repeat until there is no more input and the answer will be the [single] item remaining on the stack.